Sliding Mode Control And Observation Pdf

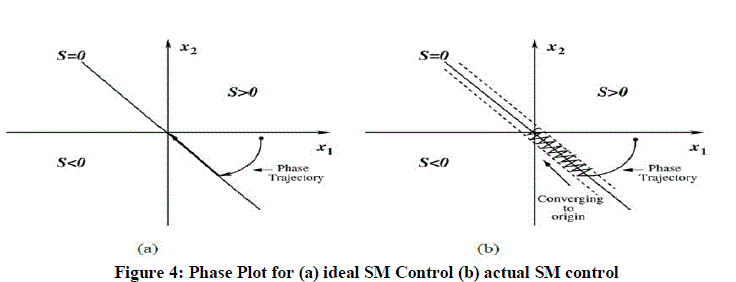
Control since a switching mode is the only operation one x Fig. Sliding mode in a variable structure system. Sliding mode in discontinuity surfaces and their intersection. Sliding mode in the intersection of discontinuity surfaces. Implementation of high-gain control via the sliding mode.

1. Sliding Mode Control Tutorial
2. Sliding Mode Control And Observation Pdf Free
3. Sliding Mode Control And Observation Pdf Pdf

The sliding mode control methodology has proven effective in dealing with complex dynamical systems affected by disturbances, uncertainties and unmodeled dynamics. Robust control technology based on this methodology has been applied to many real-world problems, especially in the areas of aerospace control, electric power systems, electromechanical systems, and robotics. Sliding Mode Control and Observation represents the first textbook that starts with classical sliding mode control techniques and progresses toward newly developed higher-order sliding mode control and observation algorithms and their applications.The present volume addresses a range of sliding mode control issues, including:*Conventional sliding mode controller and observer design*Second-order sliding mode controllers and differentiators*Frequency domain analysis of conventional and second-order sliding mode controllers*Higher-order sliding mode controllers and differentiators*Higher-order sliding mode observers*Sliding mode disturbance observer based control*Numerous applications, including reusable launch vehicle and satellite formation control, blood glucose regulation, and car steering control are used as case studiesSliding Mode Control and Observation is aimed at graduate students with a basic knowledge of classical control theory and some knowledge of state-space methods and nonlinear systems, while being of interest to a wider audience of graduate students in electrical/mechanical/aerospace engineering and applied mathematics, as well as researchers in electrical, computer, chemical, civil, mechanical, aeronautical, and industrial engineering, applied mathematicians, control engineers, and physicists. Sliding Mode Control and Observation provides the necessary tools for graduate students, researchers and engineers to robustly control complex and uncertain nonlinear dynamical systems. Exercises provided at the end of each chapter make this an ideal text for an advanced course taught in control theory.

In control theory, a state observer is a system that provides an estimate of the internal state of a given real system, from measurements of the input and output of the real system. It is typically computer-implemented, and provides the basis of many practical applications.

Knowing the system state is necessary to solve many control theory problems; for example, stabilizing a system using state feedback. In most practical cases, the physical state of the system cannot be determined by direct observation. Instead, indirect effects of the internal state are observed by way of the system outputs. A simple example is that of vehicles in a tunnel: the rates and velocities at which vehicles enter and leave the tunnel can be observed directly, but the exact state inside the tunnel can only be estimated. If a system is observable, it is possible to fully reconstruct the system state from its output measurements using the state observer.

• 1Typical observer model
• 2State observers for nonlinear systems

Typical observer model[edit]

Discrete-time case[edit]

The state of a linear, time-invariant physical discrete-time system is assumed to satisfy

x(k+1)=Ax(k)+Bu(k){displaystyle x(k+1)=Ax(k)+Bu(k)}

y(k)=Cx(k)+Du(k){displaystyle y(k)=Cx(k)+Du(k)}

where, at time k{displaystyle k}, x(k){displaystyle x(k)} is the plant's state; u(k){displaystyle u(k)} is its inputs; and y(k){displaystyle y(k)} is its outputs. These equations simply say that the plant's current outputs and its future state are both determined solely by its current states and the current inputs. (Although these equations are expressed in terms of discrete time steps, very similar equations hold for continuous systems). If this system is observable then the output of the plant, y(k){displaystyle y(k)}, can be used to steer the state of the state observer.

The observer model of the physical system is then typically derived from the above equations. Additional terms may be included in order to ensure that, on receiving successive measured values of the plant's inputs and outputs, the model's state converges to that of the plant. In particular, the output of the observer may be subtracted from the output of the plant and then multiplied by a matrix L{displaystyle L}; this is then added to the equations for the state of the observer to produce a so-called Luenberger observer, defined by the equations below. Note that the variables of a state observer are commonly denoted by a 'hat': x^(k){displaystyle {hat {x}}(k)} and y^(k){displaystyle {hat {y}}(k)} to distinguish them from the variables of the equations satisfied by the physical system.

x^(k+1)=Ax^(k)+L[y(k)−y^(k)]+Bu(k){displaystyle {hat {x}}(k+1)=A{hat {x}}(k)+Lleft[y(k)-{hat {y}}(k)right]+Bu(k)}

y^(k)=Cx^(k)+Du(k){displaystyle {hat {y}}(k)=C{hat {x}}(k)+Du(k)}

The observer is called asymptotically stable if the observer error e(k)=x^(k)−x(k){displaystyle e(k)={hat {x}}(k)-x(k)} converges to zero when k→∞{displaystyle krightarrow infty }. For a Luenberger observer, the observer error satisfies e(k+1)=(A−LC)e(k){displaystyle e(k+1)=(A-LC)e(k)}. The Luenberger observer for this discrete-time system is therefore asymptotically stable when the matrix A−LC{displaystyle A-LC} has all the eigenvalues inside the unit circle.

For control purposes the output of the observer system is fed back to the input of both the observer and the plant through the gains matrix K{displaystyle K}.

u(k)=−Kx^(k){displaystyle u(k)=-K{hat {x}}(k)}

The observer equations then become:

x^(k+1)=Ax^(k)+L(y(k)−y^(k))−BKx^(k){displaystyle {hat {x}}(k+1)=A{hat {x}}(k)+Lleft(y(k)-{hat {y}}(k)right)-BK{hat {x}}(k)}

y^(k)=Cx^(k)−DKx^(k){displaystyle {hat {y}}(k)=C{hat {x}}(k)-DK{hat {x}}(k)}

or, more simply,

x^(k+1)=(A−BK)x^(k)+L(y(k)−y^(k)){displaystyle {hat {x}}(k+1)=left(A-BKright){hat {x}}(k)+Lleft(y(k)-{hat {y}}(k)right)}

y^(k)=(C−DK)x^(k){displaystyle {hat {y}}(k)=left(C-DKright){hat {x}}(k)}

Due to the separation principle we know that we can choose K{displaystyle K} and L{displaystyle L} independently without harm to the overall stability of the systems. As a rule of thumb, the poles of the observer A−LC{displaystyle A-LC} are usually chosen to converge 10 times faster than the poles of the system A−BK{displaystyle A-BK}.

Continuous-time case[edit]

The previous example was for an observer implemented in a discrete-time LTI system. However, the process is similar for the continuous-time case; the observer gains L{displaystyle L} are chosen to make the continuous-time error dynamics converge to zero asymptotically (i.e., when A−LC{displaystyle A-LC} is a Hurwitz matrix).

For a continuous-time linear system

x˙=Ax+Bu,{displaystyle {dot {x}}=Ax+Bu,}

y=Cx+Du,{displaystyle y=Cx+Du,}

where x∈Rn,u∈Rm,y∈Rr{displaystyle xin mathbb {R} ^{n},uin mathbb {R} ^{m},yin mathbb {R} ^{r}}, the observer looks similar to discrete-time case described above:

x^˙=Ax^+Bu+L(y−y^){displaystyle {dot {hat {x}}}=A{hat {x}}+Bu+Lleft(y-{hat {y}}right)}.

y^=Cx^+Du,{displaystyle {hat {y}}=C{hat {x}}+Du,}

The observer error e=x−x^{displaystyle e=x-{hat {x}}} satisfies the equation

e˙=(A−LC)e{displaystyle {dot {e}}=(A-LC)e}.

The eigenvalues of the matrix A−LC{displaystyle A-LC} can be made arbitrarily by appropriate choice of the observer gain L{displaystyle L} when the pair [A,C]{displaystyle [A,C]} is observable, i.e. observability condition holds. In particular, it can be made Hurwitz, so the observer error e(t)→0{displaystyle e(t)rightarrow 0} when t→∞{displaystyle trightarrow infty }.

Peaking and other observer methods[edit]

When the observer gain L{displaystyle L} is high, the linear Luenberger observer converges to the system states very quickly. However, high observer gain leads to a peaking phenomenon in which initial estimator error can be prohibitively large (i.e., impractical or unsafe to use).^[1] As a consequence, nonlinear high gain observer methods are available that converge quickly without the peaking phenomenon. For example, sliding mode control can be used to design an observer that brings one estimated state's error to zero in finite time even in the presence of measurement error; the other states have error that behaves similarly to the error in a Luenberger observer after peaking has subsided. Sliding mode observers also have attractive noise resilience properties that are similar to a Kalman filter.^[2][3]Another approach is to apply multi observer, that significantly improves transients and reduces observer overshoot. Multi observer can be adapted to every system where High Gain Observer is applicable.^[4]

State observers for nonlinear systems[edit]

Sliding mode observers can be designed for the non-linear systems as well. For simplicity, first consider the no-input non-linear system:

x˙=f(x){displaystyle {dot {x}}=f(x)}

where x∈Rn{displaystyle xin mathbb {R} ^{n}}. Also assume that there is a measurable output y∈R{displaystyle yin mathbb {R} } given by

y=h(x).{displaystyle y=h(x).}

There are several non-approximate approaches for designing an observer. The two observers given below also apply to the case when the system has an input. That is,

x˙=f(x)+B(x)u,{displaystyle {dot {x}}=f(x)+B(x)u,}

y=h(x),{displaystyle y=h(x),} .

Linearizable error dynamics[edit]

One suggestion by Krener and Isidori^[5] and Krener and Respondek^[6] can be applied in a situation when there exists a linearizing transformation (i.e., a diffeomorphism, like the one used in feedback linearization) z=Φ(x){displaystyle z=Phi (x)} such that in new variables the system equations read

z˙=Az+ϕ(y),{displaystyle {dot {z}}=Az+phi (y),}

y=Cz.{displaystyle y=Cz.}

The Luenberger observer is then designed as

z^˙=Az^+ϕ(y)−L(Cz^−y){displaystyle {dot {hat {z}}}=A{hat {z}}+phi (y)-Lleft(C{hat {z}}-yright)}.

The observer error for the transformed variable e=z^−z{displaystyle e={hat {z}}-z} satisfies the same equation as in classical linear case.

e˙=(A−LC)e{displaystyle {dot {e}}=(A-LC)e}.

As shown by Gauthier, Hammouri, and Othman^[7]and Hammouri and Kinnaert,^[8] if there exists transformation z=Φ(x){displaystyle z=Phi (x)} such that the system can be transformed into the form

z˙=A(u(t))z+ϕ(y,u(t)),{displaystyle {dot {z}}=A(u(t))z+phi (y,u(t)),}

y=Cz,{displaystyle y=Cz,}

then the observer is designed as

z^˙=A(u(t))z^+ϕ(y,u(t))−L(t)(Cz^−y){displaystyle {dot {hat {z}}}=A(u(t)){hat {z}}+phi (y,u(t))-L(t)left(C{hat {z}}-yright)},

where L(t){displaystyle L(t)} is a time-varying observer gain.

Ciccarella, Dalla Mora, and Germani ^[9] obtained more advanced and general results, removing the need for a nonlinear transform and proving global asymptotic convergence of the estimated state to the true state using only simple assumptions on regularity.

Sliding mode observer[edit]

As discussed for the linear case above, the peaking phenomenon present in Luenberger observers justifies the use of a sliding mode observer. The sliding mode observer uses non-linear high-gain feedback to drive estimated states to a hypersurface where there is no difference between the estimated output and the measured output. The non-linear gain used in the observer is typically implemented with a scaled switching function, like the signum (i.e., sgn) of the estimated – measured output error. Hence, due to this high-gain feedback, the vector field of the observer has a crease in it so that observer trajectories slide along a curve where the estimated output matches the measured output exactly. So, if the system is observable from its output, the observer states will all be driven to the actual system states. Additionally, by using the sign of the error to drive the sliding mode observer, the observer trajectories become insensitive to many forms of noise. Hence, some sliding mode observers have attractive properties similar to the Kalman filter but with simpler implementation.^[2][3]

As suggested by Drakunov,^[10] a sliding mode observer can also be designed for a class of non-linear systems. Such an observer can be written in terms of original variable estimate x^{displaystyle {hat {x}}} and has the form

x^˙=[∂H(x^)∂x]−1M(x^)sgn⁡(V(t)−H(x^)){displaystyle {dot {hat {x}}}=left[{frac {partial H({hat {x}})}{partial x}}right]^{-1}M({hat {x}}),operatorname {sgn} (V(t)-H({hat {x}}))}

where:

• The sgn⁡(⋅){displaystyle operatorname {sgn} ({mathord {cdot }})} vector extends the scalar signum function to n{displaystyle n} dimensions. That is,

sgn⁡(z)=[sgn⁡(z1)sgn⁡(z2)⋮sgn⁡(zi)⋮sgn⁡(zn)]{displaystyle operatorname {sgn} (z)={begin{bmatrix}operatorname {sgn} (z_{1})operatorname {sgn} (z_{2})vdots operatorname {sgn} (z_{i})vdots operatorname {sgn} (z_{n})end{bmatrix}}}

for the vector z∈Rn{displaystyle zin mathbb {R} ^{n}}.

• The vector H(x){displaystyle H(x)} has components that are the output function h(x){displaystyle h(x)} and its repeated Lie derivatives. In particular,

H(x)≜[h1(x)h2(x)h3(x)⋮hn(x)]≜[h(x)Lfh(x)Lf2h(x)⋮Lfn−1h(x)]{displaystyle H(x)triangleq {begin{bmatrix}h_{1}(x)h_{2}(x)h_{3}(x)vdots h_{n}(x)end{bmatrix}}triangleq {begin{bmatrix}h(x)L_{f}h(x)L_{f}^{2}h(x)vdots L_{f}^{n-1}h(x)end{bmatrix}}}

where Lfih{displaystyle L_{f}^{i}h} is the i^thLie derivative of output function h{displaystyle h} along the vector field f{displaystyle f} (i.e., along x{displaystyle x} trajectories of the non-linear system). In the special case where the system has no input or has a relative degree of n, H(x(t)){displaystyle H(x(t))} is a collection of the output y(t)=h(x(t)){displaystyle y(t)=h(x(t))} and its n−1{displaystyle n-1} derivatives. Because the inverse of the Jacobian linearization of H(x){displaystyle H(x)} must exist for this observer to be well defined, the transformation H(x){displaystyle H(x)} is guaranteed to be a local diffeomorphism.

• The diagonal matrixM(x^){displaystyle M({hat {x}})} of gains is such that

M(x^)≜diag⁡(m1(x^),m2(x^),…,mn(x^))=[m1(x^)m2(x^)⋱mi(x^)⋱mn(x^)]{displaystyle M({hat {x}})triangleq operatorname {diag} (m_{1}({hat {x}}),m_{2}({hat {x}}),ldots ,m_{n}({hat {x}}))={begin{bmatrix}m_{1}({hat {x}})&&&&&&m_{2}({hat {x}})&&&&&&ddots &&&&&&m_{i}({hat {x}})&&&&&&ddots &&&&&&m_{n}({hat {x}})end{bmatrix}}}

where, for each i∈{1,2,…,n}{displaystyle iin {1,2,dots ,n}}, element mi(x^)>0{displaystyle m_{i}({hat {x}})>0} and suitably large to ensure reachability of the sliding mode.

• The observer vector V(t){displaystyle V(t)} is such that

V(t)≜[v1(t)v2(t)v3(t)⋮vi(t)⋮vn(t)]≜[y(t){m1(x^)sgn⁡(v1(t)−h1(x^(t)))}eq{m2(x^)sgn⁡(v2(t)−h2(x^(t)))}eq⋮{mi−1(x^)sgn⁡(vi−1(t)−hi−1(x^(t)))}eq⋮{mn−1(x^)sgn⁡(vn−1(t)−hn−1(x^(t)))}eq]{displaystyle V(t)triangleq {begin{bmatrix}v_{1}(t)v_{2}(t)v_{3}(t)vdots v_{i}(t)vdots v_{n}(t)end{bmatrix}}triangleq {begin{bmatrix}y(t){m_{1}({hat {x}})operatorname {sgn} (v_{1}(t)-h_{1}({hat {x}}(t)))}_{text{eq}}{m_{2}({hat {x}})operatorname {sgn} (v_{2}(t)-h_{2}({hat {x}}(t)))}_{text{eq}}vdots {m_{i-1}({hat {x}})operatorname {sgn} (v_{i-1}(t)-h_{i-1}({hat {x}}(t)))}_{text{eq}}vdots {m_{n-1}({hat {x}})operatorname {sgn} (v_{n-1}(t)-h_{n-1}({hat {x}}(t)))}_{text{eq}}end{bmatrix}}}

where sgn⁡(⋅){displaystyle operatorname {sgn} ({mathord {cdot }})} here is the normal signum function defined for scalars, and {…}eq{displaystyle {ldots }_{text{eq}}} denotes an 'equivalent value operator' of a discontinuous function in sliding mode.

The idea can be briefly explained as follows. According to the theory of sliding modes, in order to describe the system behavior, once sliding mode starts, the function sgn⁡(vi(t)−hi(x^(t))){displaystyle operatorname {sgn} (v_{i}(t)!-!h_{i}({hat {x}}(t)))} should be replaced by equivalent values (see equivalent control in the theory of sliding modes). In practice, it switches (chatters) with high frequency with slow component being equal to the equivalent value. Applying appropriate lowpass filter to get rid of the high frequency component on can obtain the value of the equivalent control, which contains more information about the state of the estimated system. The observer described above uses this method several times to obtain the state of the nonlinear system ideally in finite time.

The modified observation error can be written in the transformed states e=H(x)−H(x^){displaystyle e=H(x)-H({hat {x}})}. In particular,

{e˙=dd⁡tH(x)−dd⁡tH(x^)=dd⁡tH(x)−M(x^)sgn⁡(V(t)−H(x^(t))),{displaystyle {begin{cases}{dot {e}}={frac {operatorname {d} }{operatorname {d} t}}H(x)-{frac {operatorname {d} }{operatorname {d} t}}H({hat {x}})={frac {operatorname {d} }{operatorname {d} t}}H(x)-M({hat {x}}),operatorname {sgn} (V(t)-H({hat {x}}(t))),end{cases}}}

and so

{[e˙1e˙2⋮e˙i⋮e˙n−1e˙n]=[h˙1(x)h˙2(x)⋮h˙i(x)⋮h˙n−1(x)h˙n(x)]⏞dd⁡tH(x)−M(x^)sgn⁡(V(t)−H(x^(t)))⏞dd⁡tH(x^)=[h2(x)h3(x)⋮hi+1(x)⋮hn(x)Lfnh(x)]−[m1sgn⁡(v1(t)−h1(x^(t)))m2sgn⁡(v2(t)−h2(x^(t)))⋮misgn⁡(vi(t)−hi(x^(t)))⋮mn−1sgn⁡(vn−1(t)−hn−1(x^(t)))mnsgn⁡(vn(t)−hn(x^(t)))]=[h2(x)−m1(x^)sgn⁡(v1(t)⏞v1(t)=y(t)=h1(x)−h1(x^(t))⏞e1)h3(x)−m2(x^)sgn⁡(v2(t)−h2(x^(t)))⋮hi+1(x)−mi(x^)sgn⁡(vi(t)−hi(x^(t)))⋮hn(x)−mn−1(x^)sgn⁡(vn−1(t)−hn−1(x^(t)))Lfnh(x)−mn(x^)sgn⁡(vn(t)−hn(x^(t)))].{displaystyle {begin{cases}{begin{bmatrix}{dot {e}}_{1}{dot {e}}_{2}vdots {dot {e}}_{i}vdots {dot {e}}_{n-1}{dot {e}}_{n}end{bmatrix}}={mathord {overbrace {begin{bmatrix}{dot {h}}_{1}(x){dot {h}}_{2}(x)vdots {dot {h}}_{i}(x)vdots {dot {h}}_{n-1}(x){dot {h}}_{n}(x)end{bmatrix}} ^{{tfrac {operatorname {d} }{operatorname {d} t}}H(x)}}}-{mathord {overbrace {M({hat {x}}),operatorname {sgn} (V(t)-H({hat {x}}(t)))} ^{{tfrac {operatorname {d} }{operatorname {d} t}}H({hat {x}})}}}={begin{bmatrix}h_{2}(x)h_{3}(x)vdots h_{i+1}(x)vdots h_{n}(x)L_{f}^{n}h(x)end{bmatrix}}-{begin{bmatrix}m_{1}operatorname {sgn} (v_{1}(t)-h_{1}({hat {x}}(t)))m_{2}operatorname {sgn} (v_{2}(t)-h_{2}({hat {x}}(t)))vdots m_{i}operatorname {sgn} (v_{i}(t)-h_{i}({hat {x}}(t)))vdots m_{n-1}operatorname {sgn} (v_{n-1}(t)-h_{n-1}({hat {x}}(t)))m_{n}operatorname {sgn} (v_{n}(t)-h_{n}({hat {x}}(t)))end{bmatrix}}={begin{bmatrix}h_{2}(x)-m_{1}({hat {x}})operatorname {sgn} ({mathord {overbrace {{mathord {overbrace {v_{1}(t)} ^{v_{1}(t)=y(t)=h_{1}(x)}}}-h_{1}({hat {x}}(t))} ^{e_{1}}}})h_{3}(x)-m_{2}({hat {x}})operatorname {sgn} (v_{2}(t)-h_{2}({hat {x}}(t)))vdots h_{i+1}(x)-m_{i}({hat {x}})operatorname {sgn} (v_{i}(t)-h_{i}({hat {x}}(t)))vdots h_{n}(x)-m_{n-1}({hat {x}})operatorname {sgn} (v_{n-1}(t)-h_{n-1}({hat {x}}(t)))L_{f}^{n}h(x)-m_{n}({hat {x}})operatorname {sgn} (v_{n}(t)-h_{n}({hat {x}}(t)))end{bmatrix}}.end{cases}}}

So:

1. As long as m1(x^)≥|h2(x(t))|{displaystyle m_{1}({hat {x}})geq |h_{2}(x(t))|}, the first row of the error dynamics, e˙1=h2(x^)−m1(x^)sgn⁡(e1){displaystyle {dot {e}}_{1}=h_{2}({hat {x}})-m_{1}({hat {x}})operatorname {sgn} (e_{1})}, will meet sufficient conditions to enter the e1=0{displaystyle e_{1}=0} sliding mode in finite time.
2. Along the e1=0{displaystyle e_{1}=0} surface, the corresponding v2(t)={m1(x^)sgn⁡(e1)}eq{displaystyle v_{2}(t)={m_{1}({hat {x}})operatorname {sgn} (e_{1})}_{text{eq}}} equivalent control will be equal to h2(x){displaystyle h_{2}(x)}, and so v2(t)−h2(x^)=h2(x)−h2(x^)=e2{displaystyle v_{2}(t)-h_{2}({hat {x}})=h_{2}(x)-h_{2}({hat {x}})=e_{2}}. Hence, so long as m2(x^)≥|h3(x(t))|{displaystyle m_{2}({hat {x}})geq |h_{3}(x(t))|}, the second row of the error dynamics, e˙2=h3(x^)−m2(x^)sgn⁡(e2){displaystyle {dot {e}}_{2}=h_{3}({hat {x}})-m_{2}({hat {x}})operatorname {sgn} (e_{2})}, will enter the e2=0{displaystyle e_{2}=0} sliding mode in finite time.
3. Along the ei=0{displaystyle e_{i}=0} surface, the corresponding vi+1(t)={…}eq{displaystyle v_{i+1}(t)={ldots }_{text{eq}}} equivalent control will be equal to hi+1(x){displaystyle h_{i+1}(x)}. Hence, so long as mi+1(x^)≥|hi+2(x(t))|{displaystyle m_{i+1}({hat {x}})geq |h_{i+2}(x(t))|}, the (i+1){displaystyle (i+1)}^th row of the error dynamics, e˙i+1=hi+2(x^)−mi+1(x^)sgn⁡(ei+1){displaystyle {dot {e}}_{i+1}=h_{i+2}({hat {x}})-m_{i+1}({hat {x}})operatorname {sgn} (e_{i+1})}, will enter the ei+1=0{displaystyle e_{i+1}=0} sliding mode in finite time.

So, for sufficiently large mi{displaystyle m_{i}} gains, all observer estimated states reach the actual states in finite time. In fact, increasing mi{displaystyle m_{i}} allows for convergence in any desired finite time so long as each |hi(x(0))|{displaystyle |h_{i}(x(0))|} function can be bounded with certainty. Hence, the requirement that the map H:Rn→Rn{displaystyle H:mathbb {R} ^{n}rightarrow mathbb {R} ^{n}} is a diffeomorphism (i.e., that its Jacobian linearization is invertible) asserts that convergence of the estimated output implies convergence of the estimated state. That is, the requirement is an observability condition.

In the case of the sliding mode observer for the system with the input, additional conditions are needed for the observation error to be independent of the input. For example, that

∂H(x)∂xB(x){displaystyle {frac {partial H(x)}{partial x}}B(x)}

does not depend on time. The observer is then

Sliding Mode Control Tutorial

x^˙=[∂H(x^)∂x]−1M(x^)sgn⁡(V(t)−H(x^))+B(x^)u.{displaystyle {dot {hat {x}}}=left[{frac {partial H({hat {x}})}{partial x}}right]^{-1}M({hat {x}})operatorname {sgn} (V(t)-H({hat {x}}))+B({hat {x}})u.}

Multi Observer[edit]

Multi observer extends High Gain Observer structure from single to multi observer, with many models working simultaneously. This has two layers: the first consists of multiple High Gain Observers with different estimation states, and the second determines the importance weights of the first layer observers. The algorithm is simple to implement and does not contain any risky operations like differentiation.^[4] The idea of multiple models was previously applied to obtain information in adaptive control.^[11]

• Multi Observer Schema

Assume that the number of High Gain Observers equals n+1

ProPresenter 6.2 Crack With Keygen. ProPresenter 6.2 Crack is a professional presentation software that can used for to make professional live presentation quickly and easily.Download Full Version with offline installer ProPresenter 6.2 Serial Key from here. Many People use this software in the world for software presentation. Templatetoaster crack Crack, templatetoaster crack Keygen, templatetoaster crack Serial, templatetoaster crack No Cd. Worship Software Reviews. ProPresenter is an incredibly powerful Mac or Windows presentation. Domdomsoft Manga Downloader 5.5.22 Full Patch is a easy manga downloader of websites. Artlantis Studio 6.5 Full Keygen. Bug Fixes: & nbsp. ProPresenter 6 Crack Keygen with Serial Key Full Free is a cross-platform (Mac and Windows) lyric and media presentation package built specifically to make high-quality live productions easy – including worship gatherings, sporting events, conferences, or studio broadcasts. Jan 19, 2019  ProPresenter 6.3.8 Crack: ProPresenter 6.3.8, ProPresenter 6.3.8 Crack, ProPresenter 6.3.8 Keygen, ProPresenter 6.3.8 Serial. Crack keygen.ms.

xk^˙(t)=Axk^(t)+Bϕ0(x^(t),u(t))−L(yk^(t)−y(t)){displaystyle {dot {hat {x_{k}}}}(t)=A{hat {x_{k}}}(t)+Bphi _{0}({hat {x}}(t),u(t))-L({hat {y_{k}}}(t)-y(t))}yk^(t)=Cxk^(t){displaystyle {hat {y_{k}}}(t)=C{hat {x_{k}}}(t)}

where k=1..n+1{displaystyle k=1..n+1} is the observer index. The first layer observers consists of the same gain L{displaystyle L} but they differ with the initial state xk(0){displaystyle x_{k}(0)}. In the second layer all xk(t){displaystyle x_{k}(t)} from k=1..n+1{displaystyle k=1..n+1} observers are combined into one to obtain single state vector estimation

Sliding Mode Control And Observation Pdf Free

yk^(t)=∑k=1n+1αk(t)xk^(t){displaystyle {hat {y_{k}}}(t)=sum limits _{k=1}^{n+1}alpha _{k}(t){hat {x_{k}}}(t)}

where αk∈R{displaystyle alpha _{k}in mathbb {R} } are weight factors. These factors are changed to provide the estimation in the second layer and to improve the observation process.

Let assume that

∑k=1n+1αk(t)ξk(t)=0{displaystyle sum limits _{k=1}^{n+1}alpha _{k}(t)xi _{k}(t)=0}

and

∑k=1n+1αk(t)=1{displaystyle sum limits _{k=1}^{n+1}alpha _{k}(t)=1}

where ξk∈Rn×1{displaystyle xi _{k}in mathbb {R} ^{ntimes 1}} is some vector that depends on kth{displaystyle kth} observer error ek(t){displaystyle e_{k}(t)}.

Some transformation yields to linear regression problem

[−ξn+1(t)]=[ξ1(t)−ξn+1(t)…ξk(t)−ξn+1(t)…ξn(t)−ξn+1(t)]T[α1(t)⋮αk(t)⋮αn(t)]{displaystyle [-xi _{n+1}(t)]=[xi _{1}(t)-xi _{n+1}(t)dots xi _{k}(t)-xi _{n+1}(t)dots xi _{n}(t)-xi _{n+1}(t)]^{T}{begin{bmatrix}alpha _{1}(t)vdots alpha _{k}(t)vdots alpha _{n}(t)end{bmatrix}}}

This formula gives possibility to estimate αk(t){displaystyle alpha _{k}(t)}. To construct mainfold we need mapping m:Rn→Rn{displaystyle m:mathbb {R} ^{n}rightarrow mathbb {R} ^{n}} between ξk(t)=m(ek(t)){displaystyle xi _{k}(t)=m(e_{k}(t))} and ensurance that ξk(t){displaystyle xi _{k}(t)} is calculable relying on measurable signals. First thing is to eliminate paeking phenomenon for αk(t){displaystyle alpha _{k}(t)} from observer error

eσ(t)=∑k=1n+1αk(t)ek(t){displaystyle e_{sigma }(t)=sum limits _{k=1}^{n+1}alpha _{k}(t)e_{k}(t)}.

Calculate n{displaystyle n} times derivative on ηk(t)=y^k(t)−y(t){displaystyle eta _{k}(t)={hat {y}}_{k}(t)-y(t)} to find mapping m lead to ξk(t){displaystyle xi _{k}(t)} defined as

ξk(t)=[100⋯0CL10⋯0CALCL1⋯0CA2LCALCL⋯0⋮⋮⋮⋱CAn−2LCAn−3LCAn−4L⋯1][∫t−tdtn−1⋯∫t−tdtηk(τ)dτ⋮η(t)−η(t−(n−1)td)]{displaystyle xi _{k}(t)={begin{bmatrix}1&0&0&cdots &0CL&1&0&cdots &0CAL&CL&1&cdots &0CA^{2}L&CAL&CL&cdots &0vdots &vdots &vdots &ddots CA^{n-2}L&CA^{n-3}L&CA^{n-4}L&cdots &1end{bmatrix}}{begin{bmatrix}int limits _{t-t_{d}}^{t}{{n-1} atop cdots }int limits _{t-t_{d}}^{t}eta _{k}(tau )dtau vdots eta (t)-eta (t-(n-1)t_{d})end{bmatrix}}}

where td>0{displaystyle t_{d}>0} is some time constant. Note that ξk(t){displaystyle xi _{k}(t)} relays on both ηk(t){displaystyle eta _{k}(t)} and its integrals hence it is easily available in the control system. Further αk(t){displaystyle alpha _{k}(t)} is specified by estimation law; and thus it proves that mainfold is measurable. In the second layer α^k(t){displaystyle {hat {alpha }}_{k}(t)} for k=1…n+1{displaystyle k=1dots n+1} is introduced as estimates of αk(t){displaystyle alpha _{k}(t)} coefficients. The mapping error is specified as

eξ(t)=∑k=1n+1α^k(t)ξk(t){displaystyle e_{xi }(t)=sum limits _{k=1}^{n+1}{hat {alpha }}_{k}(t)xi _{k}(t)}

where eξ(t)∈Rn×1,α^k(t)∈R{displaystyle e_{xi }(t)in mathbb {R} ^{ntimes 1},{hat {alpha }}_{k}(t)in mathbb {R} }. If coefficients α^(t){displaystyle {hat {alpha }}(t)} are equal to αk(t){displaystyle alpha _{k}(t)} , then mapping error eξ(t)=0{displaystyle e_{xi }(t)=0} Now it is possible to calculate x^{displaystyle {hat {x}}} from above equation and hence the peaking phenomenon is reduced thanks to properties of mainfold. The created mapping gives a lot of flexibility in the estimation process. Even it is possible to estimate the value of x(t){displaystyle x(t)} in the second layer and to calculate the state x{displaystyle x}.^[4]

Bounding observers[edit]

The Bounding ^[12] or Interval observers ^[13] constitute a class of observers that provide two estimationsof the state simultaneously: one of the estimations provides an upper bound on the real value of the state,whereas the second one provides a lower bound. The real value of the state is then known to be always within these twoestimations.

These bounds are very important in practical applications,^[14][15] as they make possible to know at each time the precision of the estimation.

Mathematically, two Luenberger observers can be used, if L{displaystyle L} is properly selected, using, for example, positive systems properties:^[16] one for the upper bound x^U(k){displaystyle {hat {x}}_{U}(k)} (that ensures that e(k)=x^U(k)−x(k){displaystyle e(k)={hat {x}}_{U}(k)-x(k)} converges to zero from above when k→∞{displaystyle krightarrow infty }, in the absence of noise and uncertainty), and a lower bound x^L(k){displaystyle {hat {x}}_{L}(k)} (that ensures that e(k)=x^L(k)−x(k){displaystyle e(k)={hat {x}}_{L}(k)-x(k)} converges to zero from below). That is, always x^U(k)≥x(k)≥x^L(k){displaystyle {hat {x}}_{U}(k)geq x(k)geq {hat {x}}_{L}(k)}

See also[edit]

References[edit]

In-line references

1. ^Khalil, H.K. (2002), Nonlinear Systems (3rd ed.), Upper Saddle River, NJ: Prentice Hall, ISBN978-0-13-067389-3
2. ^ ^abUtkin, Vadim; Guldner, Jürgen; Shi, Jingxin (1999), Sliding Mode Control in Electromechanical Systems, Philadelphia, PA: Taylor & Francis, Inc., ISBN978-0-7484-0116-1
3. ^ ^abDrakunov, S.V. (1983), 'An adaptive quasioptimal filter with discontinuous parameters', Automation and Remote Control, 44 (9): 1167–1175
4. ^ ^abcBernat, J.; Stepien, S. (2015), 'Multi modelling as new estimation schema for High Gain Observers', International Journal of Control, 88 (6): 1209–1222, doi:10.1080/00207179.2014.1000380
5. ^Krener, A.J.; Isidori, Alberto (1983), 'Linearization by output injection and nonlinear observers', System and Control Letters, 3: 47–52, doi:10.1016/0167-6911(83)90037-3
6. ^Krener, A.J.; Respondek, W. (1985), 'Nonlinear observers with linearizable error dynamics', SIAM Journal on Control and Optimization, 23 (2): 197–216, doi:10.1137/0323016
7. ^Gauthier, J.P.; Hammouri, H.; Othman, S. (1992), 'A simple observer for nonlinear systems applications to bioreactors', IEEE Transactions on Automatic Control, 37 (6): 875–880, doi:10.1109/9.256352
8. ^Hammouri, H.; Kinnaert, M. (1996), 'A New Procedure for Time-Varying Linearization up to Output Injection', System and Control Letters, 28 (3): 151–157, doi:10.1016/0167-6911(96)00022-9
9. ^Ciccarella, G.; Dalla Mora, M.; Germani, A. (1993), 'A Luenberger-like observer for nonlinear systems', International Journal of Control, 57 (3): 537–556, doi:10.1080/00207179308934406
10. ^Drakunov, S.V. (1992), 'Sliding-Mode Observers Based on Equivalent Control Method', Proceedings of the 31st IEEE Conference on Decision and Control (CDC) (Tucson, Arizona, December 16–18): 2368–2370, doi:10.1109/CDC.1992.371368, ISBN978-0-7803-0872-5
11. ^Narendra, K.S.; Han, Z. (August 2012). 'A new approach to adaptive control using multiple models'. International Journal of Adaptive Control and Signal Processing. 26 (8): 778–799. doi:10.1002/acs.2269. ISSN1099-1115.
12. ^http://www.nt.ntnu.no/users/skoge/prost/proceedings/ecc03/pdfs/437.pdf
13. ^http://www.nt.ntnu.no/users/skoge/prost/proceedings/cdc-2008/data/papers/1446.pdf
14. ^http://www.iaeng.org/publication/WCE2010/WCE2010_pp656-661.pdf
15. ^Hadj-Sadok, M.Z.; Gouzé, J.L. (2001). 'Estimation of uncertain models of activated sludge processes with interval observers'. Journal of Process Control. 11 (3): 299–310. doi:10.1016/S0959-1524(99)00074-8.
16. ^Ait Rami, M., Tadeo, F., Helmke, U. (2011),'Positive observers for linear positive systems, and their implications',International Journal of Control 84

General references

• Sontag, Eduardo (1998), Mathematical Control Theory: Deterministic Finite Dimensional Systems. Second Edition, Springer, ISBN978-0-387-98489-6

Sliding Mode Control And Observation Pdf Pdf

Retrieved from 'https://en.wikipedia.org/w/index.php?title=State_observer&oldid=906459896'